PSU: Geometría |
Pregunta 02_2005
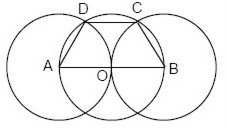
Dadas tres circunferencias congruentes, de radio 2 cm, de centros A, O y B y dos de ellas tangentes en O, como se muestra en la figura ¿cuál es el área del trapecio ABCD?
Alternativas
Clave: C
Comentario
La pregunta pertenece al contenido resolución de problemas de congruencia de figuras planas y descomposición de figuras elementales y conguentes.
Como las circunferencias de centros A y B son tangentes en O , y trazo DC es paralelo a trazo AB , porque ABCD es un trapecio, entonces los ángulos del centro OAD y OBC son iguales entre si, porque subtienden arcos congruentes.
Además, trazos
DC = AO = OB
porque
DO // CB
(ya que
![]() , pues se oponen a arcos
OC
y
AD
congruentes).
, pues se oponen a arcos
OC
y
AD
congruentes).
Luego, al unir
D
con
O
y
O
con
C
, se forman tres
triángulos equilateros
y
congruentes
entre sí por tener tres lados iguales (por el
criterio LLL
); es decir,
![]() .
.
Es así que basta calcular el área de uno de estos tres triángulos y multiplicar por 3 el valor obtenido.
En todo
triángulo equilátero
de
lado a,
cualquiera de sus alturas es igual a
![]() , luego:
, luego:
Si tomamos
Δ AOD
de base
AO = 2 cm
, su altura será
![]() .
.
Por lo que el área del
![]() .
.
Al multiplicar por 3, el área del trapecio es
![]() , por lo tanto, la
clave es C.
, por lo tanto, la
clave es C.
Otra forma de resolver este ítem es que, una vez establecida la congruencia de los triángulos, se calcule la altura del trapecio
(
![]() ).
).
Luego, aplicando la fórmula del área del trapecio, se tiene:
![]() .
.
Esta pregunta resultó muy difícil y más de un tercio de los alumnos la omiitó.
Fuente Internet:
Publicación oficial del Demre en www.demre.cl

